I. Notion d'isosurface▲
La méthode des contours duaux triangule des surfaces implicites définies sous la forme d'isosurfaces. Une surface implicite est définie indirectement : contrairement à une modélisation traditionnelle, à base de polygones et d'opérations d'extrusion, de coupe et de rétractation (réalisée dans un logiciel tel que 3ds Max ou Maya), les modèles sont définis par des expressions mathématiques.
Une isosurface est une surface définie par un potentiel (ou champ scalaire tridimensionnel) et un potentiel de référence. L'isosurface est la surface vérifiant ![]() , où U est une fonction mathématique.
, où U est une fonction mathématique.
Modéliser en utilisant des isosurfaces est très pratique et permet d'avoir facilement des surfaces lisses et de former des objets ou des personnages simples rapidement. Par exemple, une sphère de rayon![]() se modélise par une formule du type
se modélise par une formule du type ![]() (cette fonction est un polynôme : la surface est alors dite algébrique). Une formule à peine plus compliquée donne un verre à vin :
(cette fonction est un polynôme : la surface est alors dite algébrique). Une formule à peine plus compliquée donne un verre à vin :![]() (par contre, cette surface implicite n'est pas algébrique, à cause du logarithme).
(par contre, cette surface implicite n'est pas algébrique, à cause du logarithme).
La méthode du contour dual consiste d'abord à approcher la surface avec des voxels (par exemple, en sélectionnant tous les voxels traversés par l'isosurface). L'isosurface est alors approximée par le maillage de quadrangles(1) formés par les faces des voxels : il suffit alors de projeter les points qui forment les sommets des quadrangles sur l'isosurface en suivant le gradient, et c'est terminé.
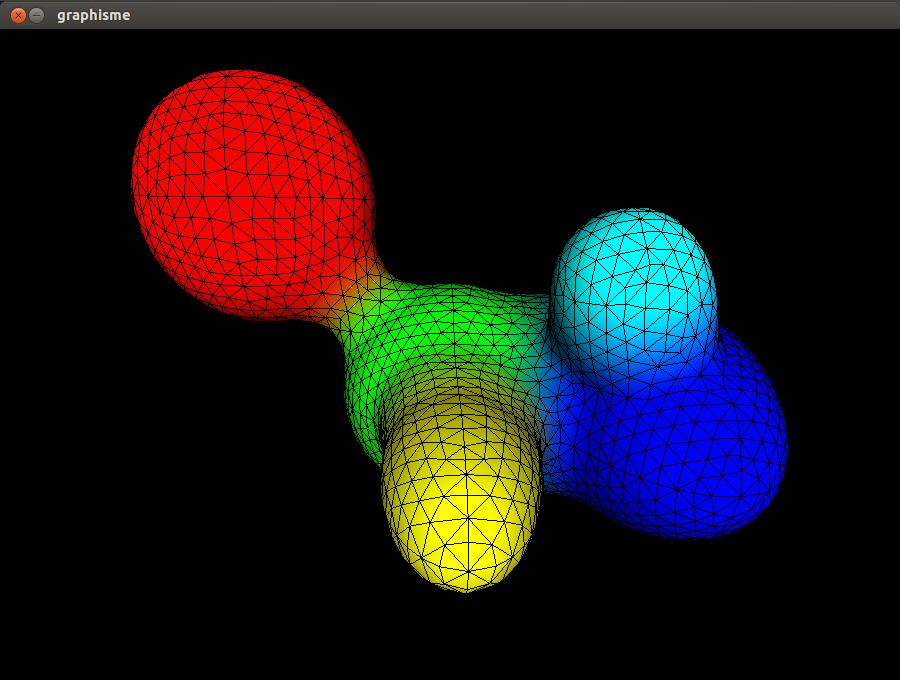
Triangulation de gouttes en temps réel
II. Les avantages de la méthode▲
La méthode du contour dual est très flexible, car elle fonctionne à partir du moment où nous pouvons définir en tout point de l'espace si nous sommes « à l'intérieur » ou « à l'extérieur » de la surface. Elle permet par exemple de réaliser des intersections de volumes. De plus, le maillage part initialement d'un contour de cubes (les voxels), ainsi ce premier maillage a de bonnes propriétés topologiques(2), ce qui rend l'algorithme stable. Lors de la projection des sommets du contour de cubes sur la surface ou isosurface, nous pouvons choisir de les placer au mieux pour approximer la surface et avoir un maillage de bonne qualité. Ainsi, des extensions au contour dual permettent de trianguler des surfaces aux bords coupants, par exemple. D'autres extensions rendent les maillages adaptatifs, en utilisant, par le biais des octrees, des voxels plus ou moins gros pour le premier maillage.
Cette méthode a donc de nombreux avantages par rapport aux autres principales méthodes plus anciennes pour trianguler les surfaces.
La croissance de triangles (marching triangles) est basée sur la triangulation de Delaunay. Cet algorithme consiste à faire grandir un maillage de triangles jusqu'à ce qu'il recouvre toute la surface implicite, tout en conservant les propriétés d'un maillage de Delaunay. Bien sûr, il faut préalablement placer un premier triangle sur l'isosurface. Cet algorithme peut donner des maillages de bonne qualité, il peut être rendu adaptatif, mais il est difficile d'obtenir des maillages grossiers et d'approximer des bords coupants. Il est donc un peu moins stable que le marching cube ou le dual contouring.
Génération de terrain et triangulation de Delaunay
Le marching cube est un algorithme de triangulation publié à l'occasion de la conférence SIGGRAPH 1987 par Lorensen et Cline. Il s'agit de trouver l'intersection de l'isosurface avec les arêtes d'une grille tridimensionnelle uniforme (donc une grille de cubes ou de voxels) et ensuite de relier les points obtenus pour former la triangulation. Cette méthode donne un maillage de mauvaise qualité avec beaucoup de triangles : il faut donc supprimer des sommets pour utiliser un tel maillage. De plus, il approxime mal la surface et les extensions (maillage adaptatif et maillage de bords coupants) sont très difficiles à réaliser sur cette méthode.
La méthode s'appelle contour dual, car elle considère d'abord le centre des voxels pour connaître leur signe, mais place les sommets sur les coins des voxels, donc sur le dual du maillage des voxels.
III. Principe du contour dual ou filet à surfaces▲
III-A. Fonctionnement de base▲
Il s'agit d'abord de trouver tous les voxels qui sont sur les bords de la surface. Pour effectuer une recherche rapide de ces voxels, il est conseillé d'utiliser un octree.
Le signe d'un voxel indique sa position par rapport à l'intérieur de l'objet à trianguler. Par convention, ce signe se définit par les règles suivantes :
- soit le potentiel au centre du voxel est supérieur au potentiel de référence, le voxel est positif ;
- soit le potentiel au centre du voxel est inférieur au potentiel de référence, le voxel est négatif.
Pour éviter de construire la surface deux fois, nous choisissons arbitrairement de sélectionner tous les voxels négatifs qui sont en contact direct avec au moins un voxel positif.
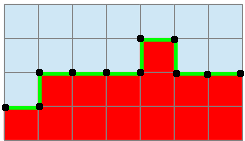
Une fois que nous avons sélectionné les voxels sur les bords, nous allons pouvoir définir la surface formée des faces carrées qui séparent chaque voxel négatif de chaque voxel positif. Ensuite, il suffit de projeter le maillage obtenu sur l'isosurface. Pour cela, nous faisons glisser les sommets qui délimitent les faces entre voxels selon le gradient du potentiel de l'isosurface jusqu'à ce que le sommet intersecte l'isosurface.
Et voilà, le contour dual est fait !
III-B. Amélioration simple▲
Le contour brut obtenu est joli, mais nous pouvons faire mieux : certains sommets sont quasiment superposés et des faces sont écrasées.
|
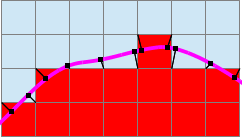
Nous allons replacer les sommets de façon à ce qu'ils soient plus écartés les uns des autres. Pour cela, rien de plus simple : pour chaque sommet, nous moyennons sa position avec le barycentre des triangles qui l'entourent et nous projetons sur l'isosurface le nouveau point obtenu. Nous obtenons alors un très beau maillage. |
Cette méthode est similaire à placer le point au barycentre de la surface qu'il forme avec les triangles qui lui appartiennent. Ainsi, le point aura tendance à s'éloigner de tout bord, donc à s'éloigner de tout autre sommet trop proche.
L'idée originelle de cette amélioration est de réaliser le dual du maillage (dual comme la triangulation de Delaunay l'est au diagramme de Voronoï) afin d'obtenir un maillage plus régulier. Cependant, les meilleurs résultats du contour dual proviennent surtout du placement des points : nous plaçons les points au centre des faces ; ainsi, nous réalisons un barycentre. Cependant, en réalisant alors le dual du dual, nous améliorons encore le maillage. Toutefois, le dual du dual donne le contour initial. Il suffit donc de réaliser le barycentre des faces autour des points pour effectuer la même opération que la dualisation du dual.
Nous pourrions essayer d'itérer le processus, mais, en pratique, il suffit de le faire une seule fois pour obtenir un beau maillage.
III-C. Erreur topologique▲
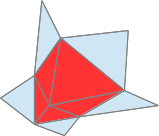
Il peut y avoir une ambiguïté qui arrive souvent sur les points de selle de l'isosurface, c'est-à-dire lorsque deux voxels en diagonale sont négatifs et que les deux voxels sur la diagonale opposée sont positifs. Il y a alors quatre faces en contact au lieu de deux.
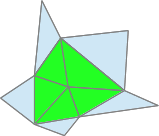
La solution est alors de fusionner les deux sommets qui séparent les quatre faces (vertex collapsing).
IV. Implémentation▲
Dans cette partie, nous développons plus concrètement la mise en pratique de l'algorithme. Elle n'est pas relative à un langage de programmation ; toutefois, le code source fourni en annexe est en C++.
IV-A. Octree (arbre octaire)▲
Il est très important d'utiliser des arbres de recherche. En effet, si nous considérons une grille périodique simple de voxels, nous arrivons très vite à un temps de construction énorme (si nous voulons un maillage fin et que nous prenons par exemple une grille de 1000 × 1000 × 1000 voxels, nous devrons tester un milliard de voxels, soit calculer le potentiel plusieurs milliards de fois). Les temps de calcul obtenus atteignent une heure avec une consommation mémoire de 8 Go. Il est possible de faire mieux !
Avec les octrees, seuls les voxels proches de la surface sont considérés. Il suffit de détecter la surface avec une grille grossière par exemple, puis de reconstituer la surface de proche en proche. Cette opération est finalement peu coûteuse et efficace. Nous pouvons même mailler en temps réel des potentiels mouvants. Par exemple, sur un processeur Intel Core i5-3230M à 2,6GHz, la construction du maillage va jusqu'à 200 000 sommets/s avec un potentiel formé de cinq gouttes et jusqu'à 500 000 sommets/s avec une seule goutte.
Un peu de vocabulaire sur les arbres de recherche :
- une feuille est un élément de l'arbre qui n'a pas de fils ;
- un nœud est un élément de l'arbre.
Il n'y aura pas de différence de structure dans notre implémentation entre une feuille et un nœud.
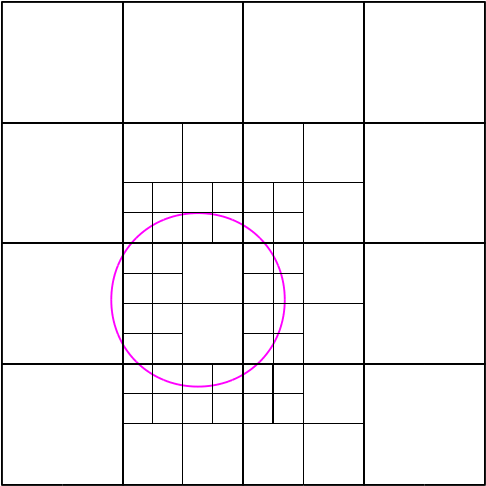
Une première grille grossière sous forme d'octree détectera la surface en appliquant récursivement l'opération : tant que les huit coins d'un cube de l'octree ont un signe différent, nous le subdivisons et nous testons ses enfants ; si le cube a la taille minimale, nous ne le subdivisons pas.
Détection de la surface, ici schématisée en 2D.
IV-B. Sélection et propagation des voxels▲
Nous avons ainsi des voxels susceptibles d'être en bordure de surface au niveau des feuilles de l'octree. Il n'y a plus qu'à les tester. Cependant, l'opération précédente ne détecte pas tous les voxels qui doivent être sélectionnés : nous voyons que le côté gauche du cercle n'est pas subdivisé comme il le devrait sur la figure ci-dessus. En effet, comme les quatre coins du carré de droite sont hors du cercle, ils sont donc de même signe et le carré n'a pas été subdivisé. Nous allons donc aussi propager le front de voxels sélectionnés.
De plus, la méthode de propagation permet, à partir du moment où l'on connaît un seul point de la surface, de la reconstruire entièrement, sans avoir besoin de réaliser une première détection de la surface avec une grille. Cela rappelle la méthode du marching triangle.
|
|
|
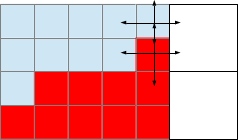
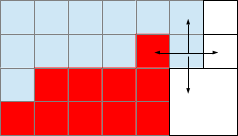
Deux étapes de la propagation des voxels.
Pour cette propagation, nous sélectionnons le voxel s'il est négatif et a au moins un voisin positif. Nous plaçons dans un tas ou un tableau les coordonnées de ses voxels voisins s'il a au moins un voisin de polarité différente de lui-même. Ce tas de coordonnées permettra de tester tous les voxels oubliés et de propager le front. Nous allons vider le tas, en testant successivement les voxels du tas, jusqu'à ce qu'il soit vide.
IV-C. Placement des sommets et des faces▲
Les sommets des carrés formés par les faces des voxels peuvent se situer aux huit coins des voxels. Cependant, il ne faut pas recréer les quatre sommets à chaque fois que nous créons un carré. Ainsi, il faut savoir si le sommet existe déjà avant de le créer. Le meilleur moyen pour empêcher les doublons est de stocker un sommet par voxel ; on prendra comme convention que le sommet relatif à un voxel est celui situé au coin de coordonnées (-1/2,-1/2,-1/2) si le voxel a une taille de 1 × 1 × 1.
Quand, par exemple, un voxel sélectionné veut créer ses faces et qu'il a besoin du sommet situé au coin de coordonnées (+1/2,+1/2,-1/2) dans le repère du voxel, il ira le chercher dans le voxel situé à (1,1,0) de lui-même. Si celui-ci n'est pas alloué, nous l'allouons et nous plaçons l'indice du sommet créé dans le voxel dans lequel il doit être. De plus, quand nous allouons le sommet, nous définissons ses coordonnées grâce aux coordonnées du coin du voxel et nous le projetons sur la surface.
Pour projeter le vecteur, nous devons en fait résoudre une équation souvent non linéaire, trouver le point P tel que P soit sur la surface, connaissant un point P0 proche de la surface (le point initial). C'est-à-dire résoudre l'équation ![]() .
.
La méthode de Newton est adaptée à ce genre de résolution :
![]() avec
avec ![]() le point initial.
le point initial.
Nous calculons le gradient par différence finie (dl assez petit pour bien approximer la dérivée, mais pas trop pour éviter les erreurs d'arrondi).
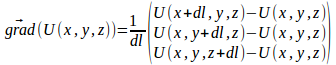
Enfin, pour mailler les quadrangles une fois projetés, nous choisissons de former les triangles qui forment la diagonale la plus courte.
|
|
|
Schéma du contour en 2D des voxels et sa projection sur la surface.
IV-D. Traitement du problème au point de selle▲
Nous allons revenir dans l'étape de sélection pour traiter le problème d'ambiguïté qui arrive lorsque deux voxels en diagonale sont négatifs et que les deux voxels dans la diagonale perpendiculaire sont positifs. Dans ce cas, nous fusionnons les deux sommets de l'arête commune aux deux voxels. Il vaut mieux fusionner ces deux sommets au début de l'algorithme pour éviter les recherches et suppressions dans les tableaux finals des sommets et triangles.
Pour fusionner de tels sommets, nous préallouons un sommet qui sera à la fois les deux sommets de l'arête commune aux deux voxels et nous mettons l'indice de ce sommet dans les voxels relatifs à l'un et l'autre sommet. La position de ce sommet est calculée à partir du milieu du segment qui a été réduit à un point.
Si nous ne faisons rien de plus, le reste du programme triangulera les faces sans se soucier que certains indices ont été fusionnés et soient identiques, il va donc créer des triangles plats. Pour y remédier, lors de la création des triangles, nous effectuons un test pour savoir si un triangle a deux fois le même sommet. Si c'est le cas, nous ne le créons pas.
IV-E. Amélioration du placement des sommets▲
Nous allons replacer les sommets pour que le maillage soit plus uniforme, de manière à éviter les triangles plats et les sommets superposés. Pour cela, nous moyennons la position du sommet avec le barycentre des triangles qui l'entourent. En notant Gi les barycentres des triangles autour du point Pj et Ai, Bi, Ci les sommets relatifs au triangle i :
![]() avec
avec![]()
Il nous suffit de calculer dans un tableau la somme des Gi et dans un autre tableau les nombres de termes n intervenant dans la somme en parcourant en une seule fois le tableau des triangles. Puis nous divisons les sommes par leur nombre de termes, et nous obtenons les nouveaux sommets. Nous projetons ensuite les vecteurs obtenus sur la surface.
|
|
|
La nouvelle position du vecteur au centre de la surface rouge est le barycentre des triangles colorés en rouge.
IV-F. Structures de données▲
Nous définissons une structure ou classe dans laquelle nous mettons tous les objets dont nous avons besoin pour réaliser le contour, les voici :
- le tableau des sommets (un tableau dynamique) ;
- le tableau des triangles (un tableau dynamique) ;
- le potentiel, une fonction qui associe une valeur numérique à tout point de l'espace ;
- le potentiel de référence, un réel ;
- un octree de voxels ;
- la taille ou profondeur d'un voxel, un entier ;
-
le tas des voxels à tester qui peut être un tableau dynamique.
Un sommet est un vecteur de trois réels et un triangle est un vecteur de trois entiers comprenant les indices des sommets du triangle dans le tableau des sommets. Les tableaux des sommets et des triangles sont particulièrement adaptés pour l'affichage avec le processeur graphique. Nous pouvons ajouter à la structure de sommet la normale au sommet et la couleur du sommet pour un affichage plus complet sous OpenGL par exemple.
Il y a un voxel par élément de l'octree. La structure de voxel doit posséder plusieurs informations :
-
l'indice du sommet relatif au coin de ce voxel. Nous pouvons prendre en convention que cet indice soit égal à -1 tant qu'il n'a pas été défini ;
-
un booléen qui indique si le voxel a déjà été testé.
Nous pouvons aussi ajouter d'autres éléments dans la structure de voxel pour diminuer le nombre d'appels à la fonction de potentiel et, ainsi, diminuer le nombre de tests inutiles. Ces éléments sont du type booléen et peuvent tenir dans un seul entier.
-
Un booléen pour savoir si le voxel est déjà dans le tas pour éviter de l'y remettre.
- Les faces à trianguler du voxel (6 booléens pour les 6 faces possibles). Cette information est utile si nous différons la sélection des voxels de la triangulation des faces.
IV-G. Affichage▲
Nous affichons notre figure avec OpenGL GLEW. Nous calculons la normale des sommets grâce au gradient du potentiel que nous renormons.
Nous donnons une couleur à chaque sommet en utilisant le principe des gouttes, mais, cette fois, au lieu d'avoir un champ scalaire, nous avons un champ vectoriel, dont les trois coordonnées du vecteur donnent respectivement les composantes bleu, vert et rouge.
V. Conclusion▲
Nous avons effectué un algorithme de triangulation de surfaces implicites suffisamment rapide pour mailler des surfaces en temps réel. De plus, en considérant l'espace fait de voxels, le contour apparaît intuitivement. L'écartement des sommets grâce au calcul d'un simple barycentre permet d'obtenir un maillage régulier.
Cet algorithme est finalement simple et puissant. Nous pouvons en faire des variantes, comme le traitement des bords coupants grâce à l'utilisation d'erreurs quadratiques qui sont minimisées lorsque les segments du maillage sont parallèles à la surface. Nous pouvons aussi utiliser des tailles de voxel variables en fonction de la courbure de l'isosurface pour obtenir un maillage adaptatif.
![]() Dual Contouring of Hermite Data
Dual Contouring of Hermite Data
Il est donc une bonne base pour réaliser des algorithmes de triangulation plus complets.
VI. Sources C++▲
Voici la liste des fichiers sources :
- matr9f.h et matr9f.cpp : comprend l'implémentation d'un vecteur de trois flottants et d'une matrice de 3 × 3 flottants ;
- octree.h : Le template pour les octrees ;
- patrons.h : tableau dynamique et quelques macros ;
- contour_dual.h et contour_dual.cpp : calcul et affichage d'isosurfaces ;
- affichable.h et affichable.cpp : affichage des segments et des points ;
- potentiel.h et potentiel.cpp : potentiel de gouttes ;
- main.cpp : affiche par défaut des gouttes mouvantes.
Normalement, OpenGL est déjà installé sur Windows ou Linux et il suffit d'installer SDL et l'extension GLEW. Pour Linux, utilisez les dépôts pour l'installation.
Pour compiler avec gcc sous Linux, utilisez la commande :
g++ -O2 -o contour *.cpp -lSDLmain -lSDL -lGLU -lGL -lGLEW
Pour Windows, suivez les indications d'installation. Cependant le site officiel glew donne seulement la bibliothèque statique pour Visual C++. Ainsi, il faudra compiler vous-même les sources de glew si vous n'utilisez pas Visual C++.
La manière la plus facile est de compiler directement les sources glew.h et glew.c avec votre projet avec la macro « GLEW_STATIC » et de lier votre projet avec dans l'ordre : mingw32, SDLmain, SDL, opengl32, glu32.
VII. Remerciements▲
Merci à Littlewhite pour son aide dans mes débuts et tout au long de la réalisation de l'article.
Merci à dourouc05 pour ses relectures rigoureuses et approfondies et ses précieux conseils.
Merci à ClaudeLeLoup pour sa relecture orthographique.